一、摘要

本文提出了一种基于双微机电系统（MEMS）谐振器的温度传感器。在该传感器中，读出电路通过测量由具有不同温度系数的独立谐振器产生的两个时钟的频率比来估算温度。该电路采用 0.18 微米 CMOS 工艺实现，在 100Hz 带宽内实现了 20 微开尔文的分辨率，同时功耗为 19mW，分辨率品质因数（FOM）为 0.04pJK²。它使我们能够实现基于 MEMS 的可编程振荡器，在 1 秒平均时间内的阿伦偏差小于 1e-10，在−45°C 至 105°C 的温度范围内频率稳定性小于±0.1ppm。此类振荡器是电信、数据通信和精确计时应用中的关键构建模块。索引词——双微机电系统（MEMS）谐振器温度数字转换器（TDC）、基于 MEMS 的可编程振荡器、温度补偿 MEMS 振荡器（TCMO）。

二、引言 

有许多应用需要具有不同要求水平的精密振荡器，如抖动、温度变化和热瞬态期间的频率稳定性、功耗等。例如，消费电子产品，如无线 USB，需要小于±30ppm[2]，商业 GPS 要求小于±2.5ppm[3]，电信应用要求小于±0.1ppm 的频率稳定性[4]、[5]。合适的时钟通常由石英晶振或微机电系统（MEMS）谐振器制成。MEMS 技术的最新进展使得 MEMS 振荡器能够取代占据主导地位数十年的石英振荡器[6] - [14]。石英和 MEMS 提供了相似的谐振器品质因数，这是实现低相位噪声（PN）和集成相位抖动的关键参数[35]。此外，两者都可以表现出低至 1ppm/K 的温度灵敏度，这对于在整个温度范围内实现准确和稳定的时钟频率是必需的。由于 MEMS 振荡器相对于石英振荡器具有优势，其重要性日益增加[12] - [15]。例如，它们利用半导体工艺和封装，从而实现更小的尺寸和更低的成本[16]、[17]。MEMS 振荡器对冲击和振动的免疫力也更高，这使得它们成为在恶劣环境中对 PN 要求较低的应用的合适选择，例如移动设备和工业设备，在这些设备中振荡器可能会受到大量的外部振动[18]、[19]。

这两种类型的振荡器都有温度补偿和未补偿的变体。未补偿的版本通常在温度范围内稳定在几十或几百ppm 以内。要实现低于 10ppm 的稳定性，它们的频率必须在温度范围内进行补偿[9]、[15]。传统上，未补偿和补偿的石英振荡器分别称为 XOs 和 TCXOs。计时领域也将 MEMS 振荡器识别为 XOs 和 TCXOs，但偶尔也使用 MOs 和 TCMOs 这些术语，尽管后者变得不常见。

如图 1 所示，基于 MEMS 的可编程振荡器封装包含三个元件：MEMS 芯片、CMOS 芯片和引线框架。如图 2（a）所示，MEMS 芯片仅承载谐振器，而 CMOS 芯片包含电子元件，如振荡器维持电路、频率合成器和分频器，这些是维持 MEMS 谐振器的振荡并以所需频率 Fout 输出时钟所必需的，在 XO 模式下，即无温度补偿时，可以表示为：

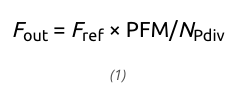
其中，Fref 是 PLL 参考时钟频率，PFM 是可编程倍频器，NPdiv 是后置分频器的值。在这种未进行温度补偿的模式下，输出时钟在温度范围内的稳定性由 MEMS 谐振器决定。本文所述的 TCXO 采用了一个温度传感器，其输出通过多项式进行适当缩放，以在每个温度下生成 Fref 的逆误差，从而调整 PFM 值以保持输出时钟频率稳定[图 2(b)]。

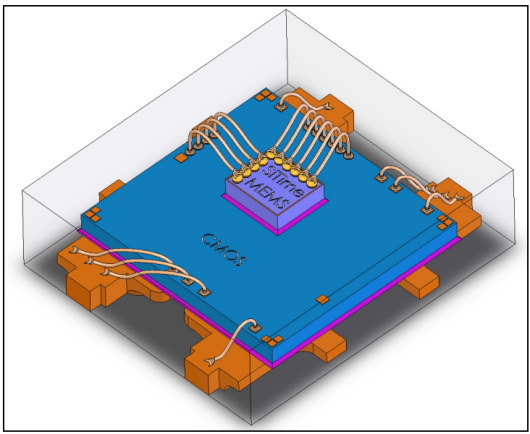
图 1. 基于 MEMS 的可编程振荡器包含一个 CMOS 芯片、一个 MEMS 芯片和一个引线框架，封装在一个单一的封装中。

因此，Fout = Fref × (1 + TDCout) × PFM/NPdiv （2），其中 TDCout 是温度数字转换器（TDC）的缩放输出。然而，这种技术引入了 TDC 作为输出时钟相位噪声（PN）的另一个贡献因素。因此，它应该具有足够的分辨率，以将其噪声保持在目标时钟抖动的可接受范围内。

在本文中，提出了一种适用于电信应用的基于 MEMS 的可编程振荡器[1]。频率合成器的参考时钟（ClkTF）由一个工作在 fTF = 47 MHz 的 Temp-Flat MEMS（MEMSTF）谐振器产生，在−45°C 至 105°C 的温度范围内表现出<±50 ppm 的频率稳定性。在该应用中，即使在振荡器经历相对快速的温度变化的微风条件下，时钟在平均时间为 1 秒时的阿伦偏差（ADEV）[20]、[21]也要求< 1e−10。 

尽管 XO 模式下的振荡器理论上满足 ADEV 要求，但由于 ClkTF 的温度灵敏度不为零，任何温度变化都会导致目标 ADEV 违规。因此，温度补偿对于实现电信应用中关键的时钟要求（在整个温度范围内频率误差< ±0.1 ppm 和 ADEV）至关重要。然而，TDC 应该具有足够的分辨率，以使它的噪声不会降低输出时钟的 PN。MEMSTF 的最大温度灵敏度为 1 ppm/K 和 ADEV 目标意味着，为了使其不主导输出时钟的 PN，其分辨率应远小于[9]。

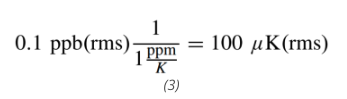
这意味着小于 50 µK 的 TDC 分辨率可确保对输出时钟 PN 的影响可忽略不计。然而，为了在存在快速温度变化的情况下保持 ADEV，应在≥100 Hz 的带宽（BW）（即转换率为 200 S/s）内实现此分辨率。假设功耗<20 mW（应用设定的另一个约束），TDC 应实现分辨率品质因数（Energy/Conversion × Resolution2）[22] <0.25 pJK2。

对于迄今为止发布的集成温度传感器，如[9]中所述，在 10 S/s 时的最佳报告分辨率为 100 µK（均方根），品质因数为 13 pJK2。它曾用于支持我们小组的上一代 MEMS 振荡器。将此工作扩展以满足目标要求将需要 1 W 的功耗。[23]中的传感器实现了迄今为止最佳的能量效率，品质因数为 0.65 pJK2，但分辨率为 10 mK（均方根），这对于我们的应用来说远远不够。此外，这两个最佳示例都是基于热敏电阻的，并且不太可能在传感器的整个寿命内满足±0.1 ppm 的稳定性要求（包括滞后）。其他 TDC 类型，例如基于 BJT 的传感器，尚未达到所需的分辨率和能量效率[22]。此类传感器的最佳报告品质因数为 3.2 pJK2，是在分辨率为 3 mK 和转换率为 455 S/s 时获得的[25]。

本文提出了一种双 MEMS 谐振器温度传感器。它在 100 Hz 的带宽内实现了 20 µK 的分辨率，同时功耗为 19 mW，分辨率品质因数为 0.04 pJK2。这是迄今为止报道的集成温度传感器的最佳能量效率。它使基于 MEMS 的可编程振荡器适用于电信应用。本文的其余部分组织如下。第二节解释了设计本文所提出的温度传感器拓扑结构的途径。第三节讨论了系统级和电路级的实现细节。第四节致力于实现和测量结果。最后，第五节给出了结论。

三、建筑设计

A.背景

如上所述，需要这种温度传感器来补偿 MEMS 谐振器在不同温度下的频率变化。为了在快速温度波动的情况下保持频率稳定性，最大化传感器前端与谐振器本身之间的热耦合非常重要。[33] 中的工作采用了一个 MEMS 谐振器，其具有两个具有不同温度系数的基本振荡模式。因此，可以通过测量每个模式的频率变化比率来确定温度。在这种架构中，传感器前端是谐振器的一部分，从而实现了紧密的热耦合。然而，这种谐振器中模态相互作用的可能性限制了设计的自由度，并且对于低相位噪声（PN）可能不是最优的。[34] 中的传感器利用了两个频率分别为 f1 和 f2 且具有不同温度系数的谐振器，封装在硅片上制造的低功耗微型烤箱中。一个锁相环（PLL）通过锁定频率为 f1 - f2 和 f1/N 的信号的相位来调节烤箱温度，其中 N 被适当选择，使得两个信号在特定温度下具有相同的频率。使用这种拓扑结构，实际上应归类为烤箱控制的 MEMS 振荡器，作者能够成功实现频率稳定性<±1 ppm。然而，与前面的示例类似，为了避免通过烤箱在谐振器之间发生模态相互作用，它们可能没有针对最佳 PN 进行优化。

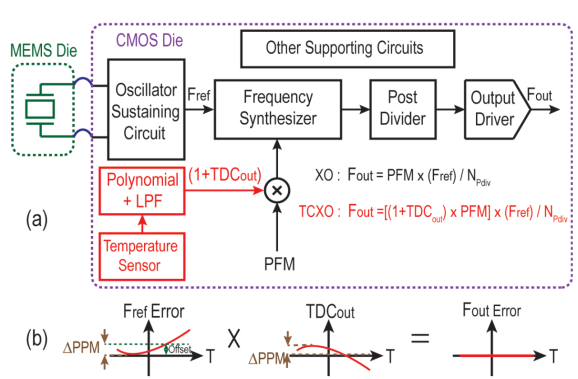
图 2.（a）在 XO 和 TCXO 模式下基于 MEMS 的可编程振荡器架构。 

（b）在 TCXO 器件中，通过将 PFM 值乘以适当缩放的 TDC 输出，输出时钟频率保持稳定。

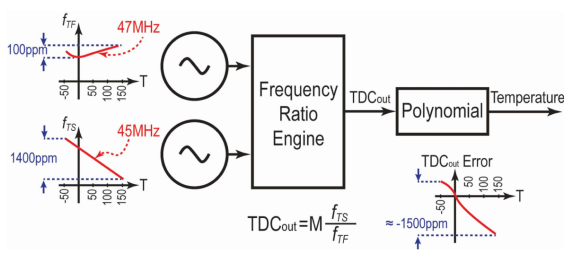
图 3. 基于测量具有不同温度系数的两个振荡器的频率比运行的温度传感器的一般架构。

如图 3 所示，测量具有不同温度敏感性的两个片上振荡器的频率比是实现温度传感器的一种众所周知的方法[26] - [28]。这种传感器的分辨率由振荡器的 PN 以及频率比引擎本身的随机和/或量化噪声决定。采用低抖动的 MEMS 生成的时钟以及低噪声频率比引擎，可以被视为实现目标分辨率的一种解决方案。因此，除了 MEMSTF 之外，还采用了温度系数为 -7 ppm / K 的 Temp-Sense MEMS（MEMSTS）谐振器来生成 ClkTS，即频率比引擎的第二个输入时钟，其振荡频率为 fTS = 45 MHz。如图 4 所示，两个谐振器并排放置，以最大程度地实现它们的热耦合。每个谐振器包括四个用于电容驱动和传感的环，并通过横梁耦合[35]。两个谐振器都实现了典型的品质因数 150,000。它们的温度敏感性通过操纵谐振器的机械特性来严格控制。在该方案中，设计 TDC 的挑战实际上归结为实现频率比引擎，其输出噪声主要由其两个输入时钟的 PNs 决定。图 5（a）说明了测量两个频率之比的最直接的架构。如图所示，在由另一个时钟（即 f2 / M [29]，[30]）的分频版本设置的门时间内，对时钟 f1 产生的周期数进行计数。因此，计数器的值与两个频率的比率成正比变化。

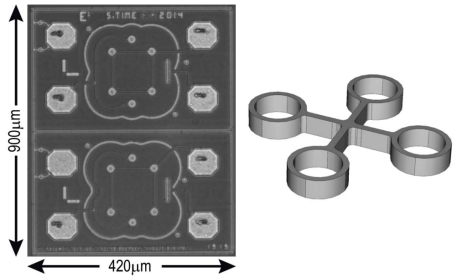
图 4. MEMSTF 和 MEMSTS 谐振器的 3D 视图和 MEMS 芯片照片

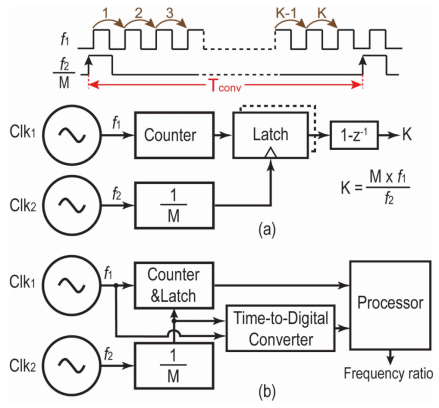
图 5.（a）倒数计数法。（b）采用时间数字转换器来提高倒数计数法的速度。

然而，这种拓扑结构实现高分辨率的速度极慢。例如，在本文中，温度变化 50 µK 会导致 ClkTS 周期 TTS 变化。

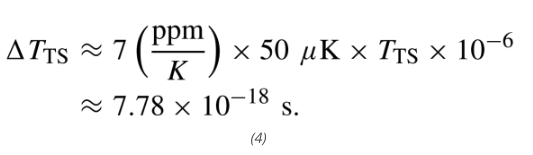
由于计数器可检测到的最小时间变化为 TTS，假设 ClkTF 的周期为 TTF，则检测如此小的温度变化所需的最小转换时间 Tconv 由下式给出：

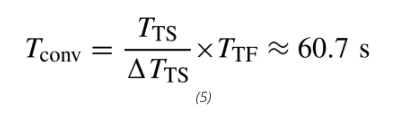
这个时间大得不切实际，在大多数应用中无法承受。

如图 5(b)所示，在另一种方法中，可以使用 TDC 来检测传感器全转换时间（例如本文中的 5 ms）内由 ΔTTS 累积的相位变化，从而得到所需的时间分辨率 Tres 为：

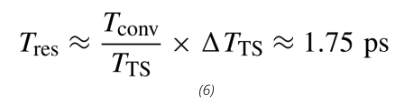
在本文所使用的 0.18 µm CMOS 工艺中，这并不容易实现。应当注意的是，（5）和（6）中的结果本身是乐观的，因为它们没有考虑两个时钟的噪声影响。一个关键的观察结果是，在这两种方法中，Clk1 和 Clk2 所有边沿的信息在采样点之间都会丢失。从信息的角度来看，当处于信号数据的极限时，信息的丢失本质上会导致性能的下降。

B. 新的频率比引擎架构  

如图 6(a) 所示，本文提出了一种新方法，该方法基于测量两个时钟上升沿之间的时间差 ΔTi 进行操作，从而利用所有转换点上可用的信息。通过使所得的 ΔT 序列通过一个最优滤波器，可以以所需的分辨率和速度测量两个频率之间的比值。最优滤波器可以是高阶低通滤波器或最小均方自适应滤波器。如图 6(b) 所示，这个想法可以通过采用高速环形振荡器，然后接两个相位量化器来实现。每个相位量化器测量环形振荡器在其输入时钟的每个周期内所经过的相位。因此，两个量化器输出之间的比值是一个无量纲数，包含了经过适当滤波后可以以目标分辨率提取的频率比信息。环形振荡器的振荡频率越高，时间数字转换器达到的分辨率就越高，从而导致更好的频率比估计。尽管这种拓扑结构工作良好，但它受到自由运行环形振荡器的所有缺点的影响，例如长时间的频率漂移。  

如图 6(c) 所示，为了克服上述问题，将自由运行的环形振荡器置于锁相环内，将其相位锁定到 ClkTF。因此，对于 ClkTS 只需要一个相位量化器，因为 ClkTF 已经与环形振荡器相位锁定。在这个方案中，相位量化器测量环形振荡器在每个 ClkTS 周期内所经过的相位，经过适当滤波后可以估计频率比。通过将环形振荡器锁定到输入时钟的缩放频率比，可以进一步提高这种可行架构的性能。如图 6(d) 所示，这种拓扑结构形成了一个以 ClkTS 为参考的新锁相环，其中另一个锁相环嵌套在其中，作为外环的数控振荡器（DCO）。为了使这个想法可行，环形振荡器必须置于分数 N 锁相环中，因为频率比是非整数量。这种拓扑结构是本文中使用的频率比引擎的核心思想，使我们能够在短的转换时间内以高分辨率测量温度。这种架构的关键优势在于它提取了两个输入时钟边沿上所有可用的温度信息，实际上，这就是它能够同时满足目标分辨率和速度规格的方式。

四、实现

图 7 展示了所提出的频率比引擎的模块级架构。它由一个参考 ClkTF 的模拟ΣΔ分数 N 锁相环嵌套在一个参考 ClkTS 的数字锁相环中组成。假设 fTF 固定，由于其输出频率 fDCO 由分数分频器输入值 DCOin（这是一个数字）设定，模拟锁相环的行为类似于 DCO。因此，fDCO = fTF × DCOin （7）。另一方面，数字锁相环采用反馈分频值 10，因此 fDCO = fTS × 10。（8）

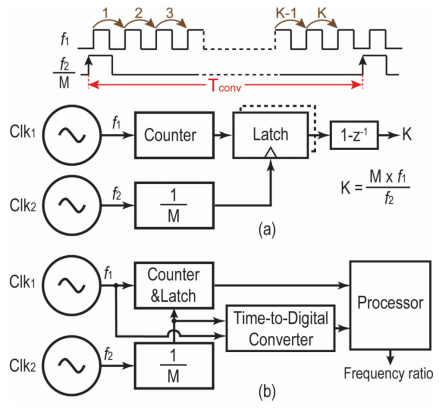
图 6. （a）基于使用时间数字转换器和滤波器计算两个时钟的频率比运行的温度传感器的架构。 

（b）通过利用环形振荡器和双相量化器实现时间数字转换器。 

（c）环形振荡器与 ClkTF 锁相。 

（d）振荡器以输入时钟频率的缩放比例运行。

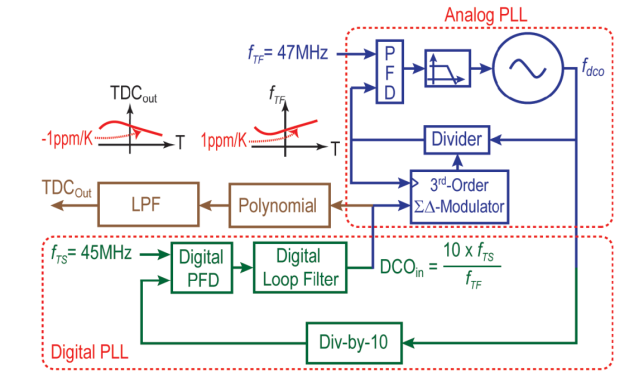
图 7. 所提出的双 MEMS 谐振器温度传感器的框图。

因此，通过结合（7）和（8），分数分频器输入值表示为

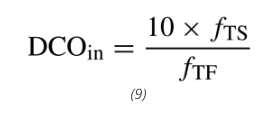
反馈回路迫使 DCOin 始终是输入时钟频率的缩放比例。因此，可以通过对 DCOin 值进行后处理来读出温度。与图 5 类似，模拟锁相环的压控振荡器（VCO）是数字相位量化器中使用的时间数字转换器的一部分。其振荡频率越高，数字鉴相器注入环路的噪声就越小。根据第四节中描述的噪声分析，10 的分频值使分辨率目标在不使数字鉴相器过于复杂的情况下得以实现，同时将 VCO 功耗保持在合理范围内。由于该温度传感器旨在补偿 MEMSTF 频率变化，如图 7 所示，其输出经过适当缩放以呈现出 fTF 误差随温度的反特性。为此，DCOin 应用于一个数字模块，即所谓的 TDC 数据路径，由一个数字七阶多项式后跟一个低通滤波器组成。多项式的阶数根据两个谐振器的非线性程度和目标输出频率稳定性来选择。在对谐振器进行全温表征后，还为每个器件单独设置了其系数。低通滤波器切除高于所需带宽的 TDC 噪声。 

B. 噪声分析和电路级实现

TDC 设计中的关键目标是频率比引擎具有足够高的带宽以跟踪快速的温度变化，同时对近距离的 TDC 输出噪声影响可忽略不计。图 8 展示了图 7 中所示的频率比引擎的模块级模型以及系统中存在的主要噪声源。如前所述，数字锁相环由时钟分频器、作为鉴相器运行的时间数字转换器、数字环路滤波器 L(z)和 DCO 组成。数字环路滤波器的输出，即频率比引擎的输出，跟踪由于环境温度波动在数字锁相环带宽内发生的 ClkTS 的相位变化。因此，该环路考虑 5 kHz 的带宽，以确保引擎对于目标温度传感器带宽足够快。DCO 是一个模拟ΣΔ分数 N 锁相环，包括异或鉴相器、环路滤波器、分数分频器和 VCO。除 ClkTF PN 外，ΣΔ调制器量化噪声以及 VCO PN 是 DCO 输出噪声的主要贡献者。在本设计中，采用三阶ΣΔ调制器既减少了分数分频器的带内噪声贡献，又增加了 DCO 的远场噪声功率，实际上使 DCO 输出时钟边沿抖动更多，从而提高了后续时间数字转换器的有效分辨率。

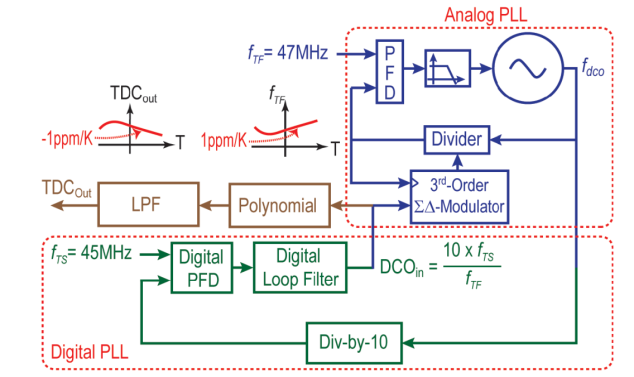
图 8. 频率比引擎的频域模型。  

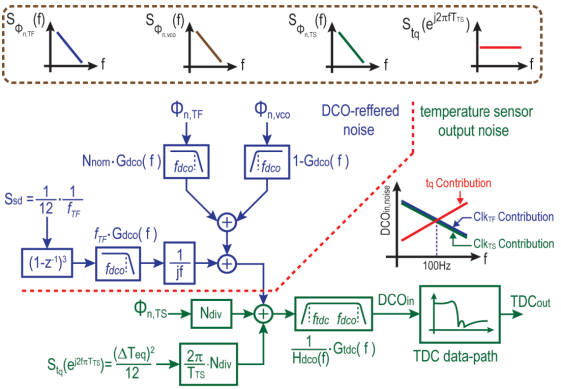
图 9. 系统中存在的主要噪声源及其对温度传感器输出的传递函数的详细视图。

图 9 展示了主要的噪声源及其在不同频率下的形状和通向 TDC 输出的传递函数[31]，其中

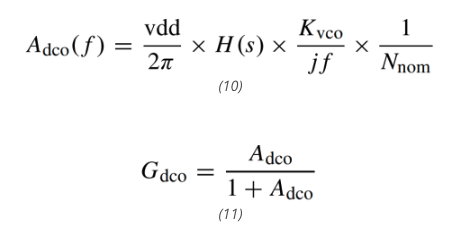
其中，Adco(f) 是模拟 PLL 环路增益，vdd 是 PFD 的电源电压，H(s) 是环路滤波器的传递函数，Nnom 是模拟 PLL 的标称分频值，Gdco(f) 是由 Adco(f) 定义的基本函数。由于 Adco(f) 在原点处有一个极点，具有低通特性，因此 Gdcoq(f) 也具有低通滤波器的形状，其带宽 DCO 环路 fdco 约为 2 MHz。DCO 的传递函数可以表示为：

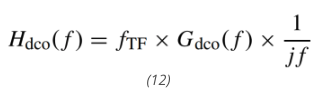
同样，数字 PLL 环路增益可以表示为：

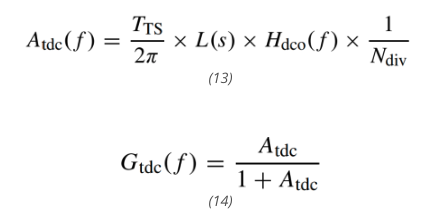
其中 L(s) 是拉普拉斯域中的数字环路滤波器传递函数，Ndiv 是分频值，在本设计中设置为 10，Gtdc(f) 是由 Atdc(f) 定义的基本函数。根据 Atdc(f) 的定义，Gtdc(f) 具有低通滤波器的形状，其带宽等于数字 PLL 带宽 ftdc，约为 5 kHz。就温度传感器而言，100 Hz 以下频率的输出噪声功率很重要。在图 8 所示的噪声源中，ΣΔ调制器噪声和 VCO 相位噪声在该范围内对输出噪声的影响最小。这是因为在 DCO 内部，前者被调制器噪声传递函数强烈整形，后者被高通传递函数衰减。它们都被从 DCO 输出到数字 PLL 环路滤波器输出的高通传递函数进一步抑制。

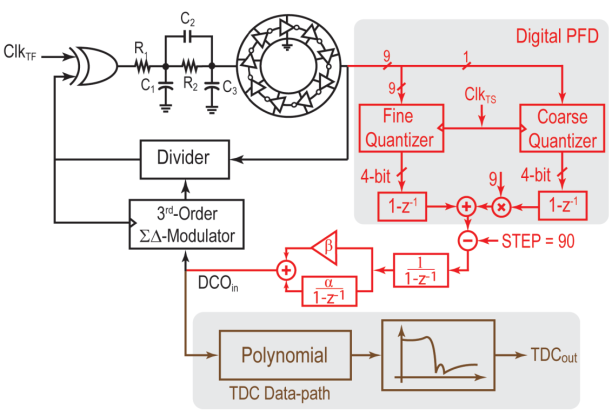
图 10. 用于实现频率比引擎和 TDC 数据路径的构建模块 

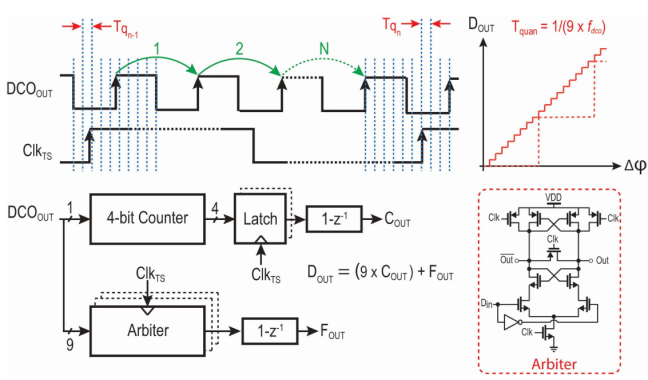
图 11. 数字 PFD 架构，由粗调部分和微调部分组成

然而，ClkTF PN∅n,TF 首先在 DCO 内被 Nnom 放大，然后被从 DCO 到引擎输出的传递函数的高通形状衰减。ClkTS PN∅n,TS 通过由数字 PLL 设置的相同传递函数，同时也被 Ndiv 增益。由于在稳态下 Ndiv 和 Nnom 的值非常接近，可以公平地说，∅n,TS 和∅n,TF 在引擎输出处具有相同的增益。最后一个噪声源是时间数字转换器的量化噪声。假定其噪声功率谱密度为(ΔTeq) 2/12，其通过的传递函数与∅n,TS 相似，但直流增益不同。因此，在非常低的频率下，这种噪声的影响可以忽略不计。然而，重要的是要确保它在传感器带宽内低于输入时钟产生的噪声。该模型建议 ΔTeq < 250 ps，以保证在低于 100 Hz 的频率下对输出噪声的影响最小。

图 10 更详细地展示了频率比引擎。数字环路中的 PFD 在每个 ClkTS 周期计算 DCO 相位变化，由粗和细两部分组成。如图 11 所示，粗量化器是一个 4 位计数器，连续对 VCO 输出的上升沿进行计数，根据（7），在锁定条件下以 450 MHz 运行，因此分辨率约为 2.22 ns。为了实现<250 ps 的分辨率，通过连接到其所有内部相位的仲裁器，在 ClkTS 的每个上升沿利用精细量化器锁存环形振荡器的状态。理论上，通过考虑 VCO 周期中每个相位的两个转换，这种配置的量化器能够实现 TVCO/2NS 的时间分辨率[32]，其中 TVCO 和 NS 分别是 VCO 的时钟周期和级数。因此，五级单端环形振荡器似乎是一个合适的选择，因为它提供了 220 ps 的分辨率。然而，在工艺、电压和温度变化时，每个级的上升到下降和下降到上升延迟之间的不平等会产生非线性量化器，并导致 DCO 输出噪声折叠到基带。为避免此问题，VCO 设计为九级，并且只考虑上升转换，因为它们的时间差在所有条件下保持恒定，约为 245 ps。如图 10 所示，粗部分的输出乘以 9 后与精细量化器的输出相加。因此，数字 PFD 输出 DOUT 可以表示为：

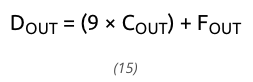
其中 COUT 和 FOUT 分别是粗量化器和精细量化器的输出。

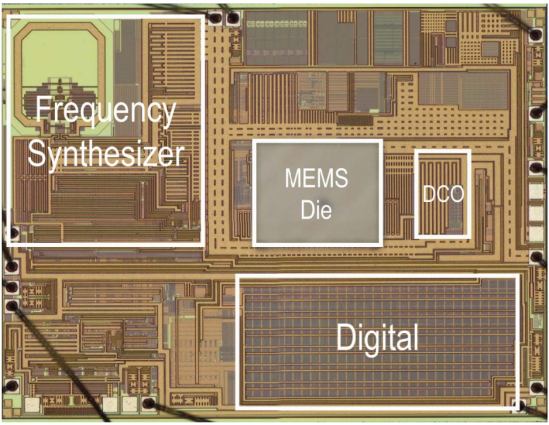
图 12. 基于 MEMS 的可编程振荡器的芯片显微照片

通过从 90 步（数字 PFD 计算的锁定条件下环形应达到的期望相位）中减去 DOUT 得到的 VCO 相位误差，然后输入到数字环路滤波器。实际上，由于数字 PLL 迫使 VCO 相位误差为零，此减法相当于除以 10。选择系数以实现 5 kHz 带宽的数字环路滤波器输出应用于 DCO 的ΣΔ调制器输入以闭合环路，并应用于 TDC 数据路径以进行进一步处理，并生成适当的校正值以补偿每个温度下的 ClkTF 频率误差。重要的是，数字电路具有足够的操作数宽度，以使截断误差不会主导 TDC 输出噪声。